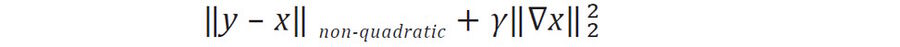现有多种成像优化去噪方法,最常用的是Rolling ball与Sliding paraboloid法 [1,2]。近期徕卡显微系统公司推出了其自主研发的成像优化技术——即时成像解析(ICC)[3],该技术已集成于所有徕卡THUNDER宽场成像平台。无论采用何种成像优化方法,均致力于在保留图像底层结构细节的同时最小化噪声与特征丢失。最重要的是,这些成像优化技术旨在提升采集数据的分析与量化精度。
常用成像优化方法
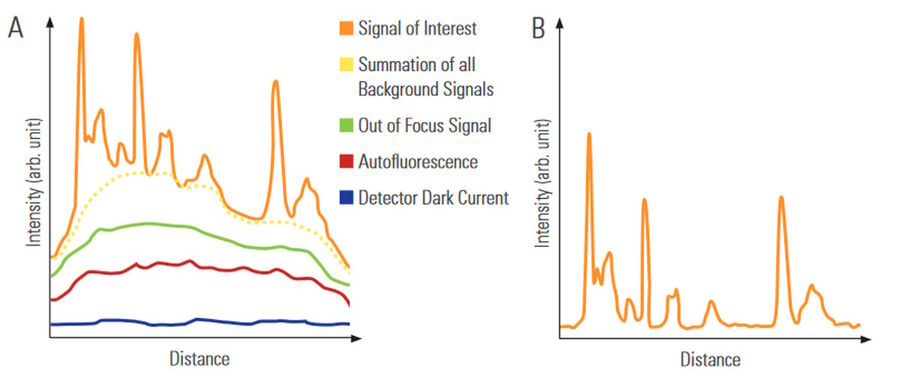
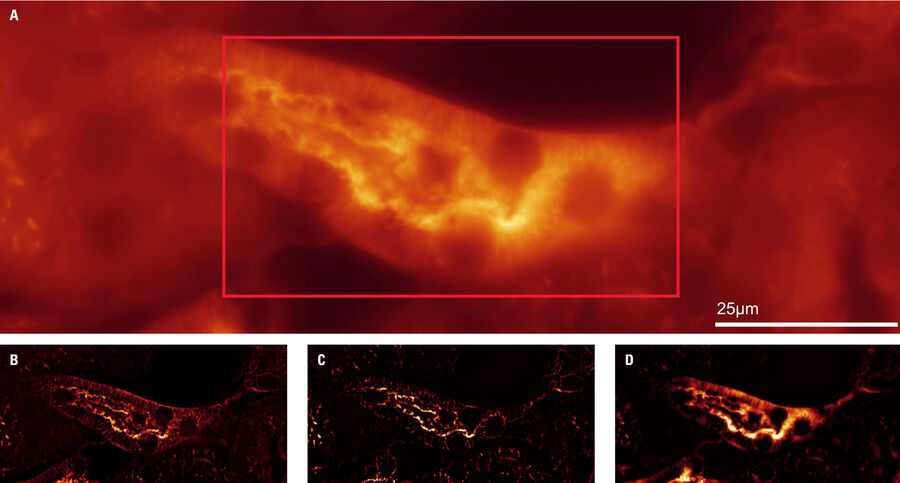
Rolling ball法(图 2C)是一种常见的成像优化方法,它通过在图像上放置一个结构元素来实现,该结构元素的球面曲率半径由用户以像素为单位设定[1,2,4]。为高效去除背景,像素半径通常设置为等于或略大于图像中最大特征的尺寸值。相对于图像中特征的强度峰值,背景被视为平滑区域;当结构元素尺寸大于特征宽度时,该元素通过改变像素的局部背景值来作用于背景。在实施Rolling ball算法前,通常会对图像应用高斯滤波器——该滤波器作为低频滤波器可平滑图像。先进行高斯滤波再执行Rolling ball处理,有助于降低图像噪声,从而获得更优的成像优化效果。
Sliding paraboloid(图 2D)是另一种常用的成像优化方法,与Rolling ball算法类似。该方法将球体替换为抛物面的顶点,并通过半径值定义抛物面的曲率[4]。通过使抛物面在图像上滑动,利用顶点处的强度变化估计局部背景并进行扣除。当图像特征与像素值对应关系不佳时,这种方法能更妥善地处理数据。其功能实现方式与Rolling ball算法相似,并可配合高斯滤波等预处理手段抑制结果图像中的噪声。
Rolling ball、Sliding paraboloid及其他成像优化方法需借助结构元素、小波变换或点扩散函数建模来估计并扣除背景[1,2,4]。为在最小化特征侵蚀的同时实现高效背景去除,参数识别过程往往耗时且需人工干预,通常作为采集后处理流程实施。徕卡显微系统公司开发的新型成像优化算法有效解决了这些难题。
徕卡的解决方案:即时成像解析
The ICC algorithm [3] offered by Leica uses a different approach to increase image contrast. ICC does not implement structural elements, wavelet transforms, or use point spread function (PSF) modeling to estimate the background noise. ICC improves image contrast by considering the entire image and applies a model to distinguish signal (structures within the image) from the background noise. Similar to minimizing a cost function [5-8] for linear regression, ICC minimizes a non-quadratic cost function to estimate the background noise, Eq 1:徕卡提供的 ICC 算法 [3]采用了一种不同的方法来增强图像对比度。该技术既不依赖结构元素或小波变换,也不通过点扩散函数(PSF)建模来估计背景噪声。ICC 通过全局分析图像并建立模型来区分图像信号(内部结构)与背景噪声,从而提升对比度。类似于线性回归中最小化代价函数[5-8]的原理,ICC 通过最小化非二次代价函数来估算背景噪声(见公式 1):
其中 y 为输入参数,x 为待估计的背景噪声,γ‖∇x‖22 表示 L2正则化项,γ为正则化参数。该参数默认设置为与光学系统点扩散函数(PSF)半高全宽成比例的固定值,或由用户根据图像中特定特征尺寸手动选择。整体而言,γ‖∇x‖22 通过惩罚代价函数来防止背景过拟合或目标特征被侵蚀。背景噪声估计完成后,将其从图像中减去即可得到真实信号(图 2B)。
结论
Rolling ball和Sliding paraboloid算法均可在第三方图像分析工具中找到,包括付费显微镜软件包及开源软件如 FIJI[4]。这些成像优化方法的具体应用方式存在差异,但通常作为成像工作流外的后处理步骤作用于原始数据。这两种成像优化方法在原始数据上的应用是一个迭代过程,需要用户确定最佳像素值以增强图像特征同时保留结构细节。相比之下,ICC 完全集成于成像工作流中实现背景噪声消除与图像对比度增强,既可在采集后应用,也可在采集过程中实时提供对比度优化图像的即时预览。ICC 处理后的原始数据保持未修改状态,便于用户进行基准真值分析。经 ICC 处理后,原始数据集与处理数据集均可通过徕卡 LASX 软件中的三维可视化及二维/三维分析模块进行进一步对比分析。
使用Rolling ball、Sliding paraboloid或即时成像解析(ICC)进行图像成像优化可提升图像清晰度,但这种改善仅限于对比度增强,对图像分辨率无影响。为提高分辨率,徕卡提供了一种自适应去卷积算法,可与 ICC 联用,使图像同时获得对比度与分辨率的提升。该算法的自适应性源于逐体素生成的自适应信噪比系数,通过正则化约束去卷积过程。关于徕卡自适应去卷积的深度探讨将在我们即将发布的技术简报中详述。