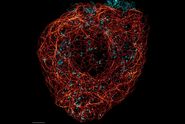
3D点扩散函数(PSF)和半高宽(FWHM)
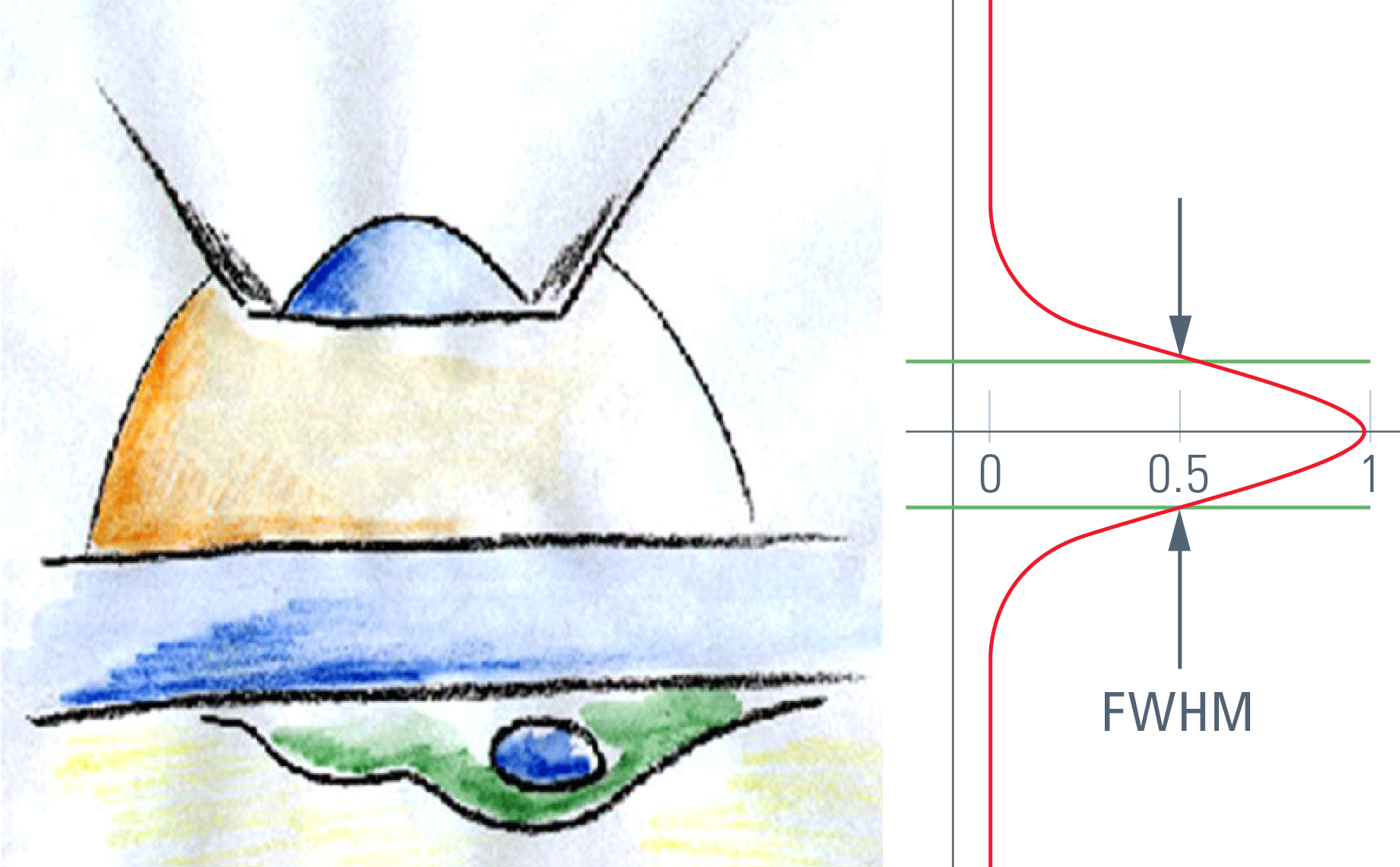
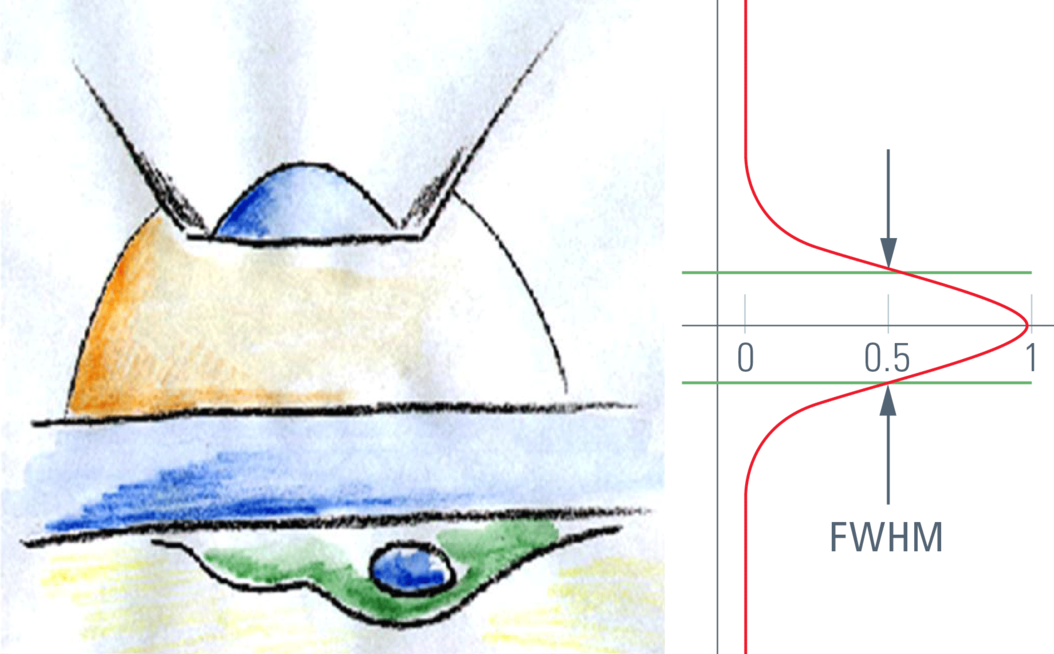
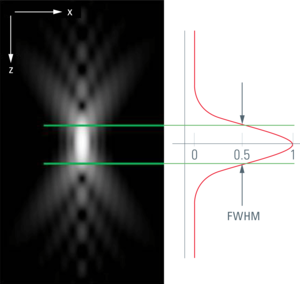
由光学系统产生的点(光斑)的图像称为“点扩散函数”(PSF)。点扩散函数描述了来自极小光斑的光在三维空间中的分布。这个衍射模型的中心是一个椭球形,影响着光学分辨率。径向尺寸决定横向分辨率,轴向尺寸决定聚焦深度,进而决定切片性能。
对于共聚焦截面切片,其目的在于只传输PSF的内核部分,即定义为光学切片。实际上,针孔直径可控制从内核外传递的光量。因此,处在衍射模型大小范围内的光学切片很明显不会出现类似于面包切片的锋利边缘,但仍然存在着同等扁平斜率的特征。连接强度曲线两侧50%强度的z距离称为“半高宽”(FWHM),而按照惯例,这是用于测量光学切片的厚度。光学切片的性能通常要通过聚焦在镜面上来进行测量,镜面用于模拟z方向上无限薄的结构。这种方法(相对而言)较容易落实并且可用于检查共聚焦显微镜系统的性能。从更为现实的角度进行考虑,z切片性能还可以通过荧光小球进行测量(见图1)。荧光小球能够在符合现实中荧光成像非相干条件下进行性能测量,因此满足了生物医学科学中的大多数共聚焦应用。反射光模式(镜面)中受衍射限制的光学切片与荧光模式的切片相比要薄得多。在比较文献中的图表时请务必牢记这一点。
控制光学切片厚度的参数
在理想条件下,可实现的最薄切片仅取决于光学衍射的限制。最明显的是波长,主要按比例控制PSF的大小:波长越短,切片越薄。我们可以假设激发光的波长有限(而不是发射光的波长),因为照明区域外并无发射光。第二个参数是物镜的光圈(数值孔径,NA):NA越高(信息收集的角度越宽),则光学切片越薄。此外,样本的折射率会影响轴向分辨率,进而影响到切片性能。图2给出了切片尺寸与这些参数的依赖关系。
第三个参数是探测路径中的针孔直径,对于上面给出的公式可假设其为零。因此,该公式给出了荧光成像的最佳值,当然这只具有理论意义:直径为零的针孔不会生成明亮的图像!
光学切片厚度的关键评论
数值孔径NA对切片厚度有显著(1/平方)影响。PSF的径向扩展与NA成线性关系。因此,对于低NA物镜,PSF内核会拉得极长,而且切片会变得很厚。因此,绝大多数应用中都是用NA>1的浸润式物镜,其中xy和z维度的比例大致接近于系数2。按照经验,高NA物镜z部分分辨率大致为xy的两倍。
理论上的考虑有助于评估光学系统的性能。实际上,仪器和样本都会导致计算数值的偏差。必须仔细校准并操作仪器才能获得最佳性能。而样本本身就是分辨率的敌人,尤其是在更深层次成像时。因此,必须特别注意折射率匹配、适宜和恒定的温度以及正确的盖玻片选择。该理论给出的是经验法则,但样本和设置可能会带来显著的偏差 —因为生物样本比晶体(或真空)更复杂,所以偏差通常也不可避免。
参考文献
- Sheppard CJR: Scanning optical microscopy. In: Barer R and Cosslett VE (eds), Advances in Optical and Electron Microscopy 10 (1987). Academic Press, London UK.
- Wilson T: Confocal Microscopy. Academic Press, London UK (1990).
- Corle TR and Kino GS: Confocal Scanning Optical Microscopy and Related Imaging Systems. Academic Press, San Diego USA (1996).
- Borlinghaus RT and Gröbler B.: Basic Principles and Applications of Confocal Laser Scanning Microscopy. In Isenberg G (ed): Modern Optics, Electronics, and High Precision Techniques in Cell Biology, 35–53 (1997). Springer Heidelberg.
- Cox G: Optical Imaging Techniques in Cell Biology. Taylor & Francis, Boca Raton USA (2007).